All Pair Shortest Path Algorithm
suggest changeFloyd-Warshall’s algorithm is for finding shortest paths in a weighted graph with positive or negative edge weights. A single execution of the algorithm will find the lengths (summed weights) of the shortest paths between all pair of vertices. With a little variation, it can print the shortest path and can detect negative cycles in a graph. Floyd-Warshall is a Dynamic-Programming algorithm.
Let’s look at an example. We’re going to apply Floyd-Warshall’s algorithm on this graph:
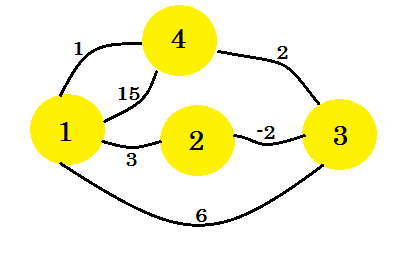
First thing we do is, we take two 2D matrices. These are adjacency matrices. The size of the matrices is going to be the total number of vertices. For our graph, we will take 4 * 4 matrices. The Distance Matrix is going to store the minimum distance found so far between two vertices. At first, for the edges, if there is an edge between u-v and the distance/weight is w, we’ll store: distance[u][v] = w. For all the edges that doesn’t exist, we’re gonna put infinity. The Path Matrix is for regenerating minimum distance path between two vertices. So initially, if there is a path between u and v, we’re going to put path[u][v] = u. This means the best way to come to vertex-v from vertex-u is to use the edge that connects v with u. If there is no path between two vertices, we’re going to put N there indicating there is no path available now. The two tables for our graph will look like:
+-----+-----+-----+-----+-----+ +-----+-----+-----+-----+-----+
| | 1 | 2 | 3 | 4 | | | 1 | 2 | 3 | 4 |
+-----+-----+-----+-----+-----+ +-----+-----+-----+-----+-----+
| 1 | 0 | 3 | 6 | 15 | | 1 | N | 1 | 1 | 1 |
+-----+-----+-----+-----+-----+ +-----+-----+-----+-----+-----+
| 2 | inf | 0 | -2 | inf | | 2 | N | N | 2 | N |
+-----+-----+-----+-----+-----+ +-----+-----+-----+-----+-----+
| 3 | inf | inf | 0 | 2 | | 3 | N | N | N | 3 |
+-----+-----+-----+-----+-----+ +-----+-----+-----+-----+-----+
| 4 | 1 | inf | inf | 0 | | 4 | 4 | N | N | N |
+-----+-----+-----+-----+-----+ +-----+-----+-----+-----+-----+
distance pathSince there is no loop, the diagonals are set N. And the distance from the vertex itself is 0.
To apply Floyd-Warshall algorithm, we’re going to select a middle vertex k. Then for each vertex i, we’re going to check if we can go from i to k and then k to j, where j is another vertex and minimize the cost of going from i to j. If the current distance[i][j] is greater than distance[i][k] + distance[k][j], we’re going to put distance[i][j] equals to the summation of those two distances. And the path[i][j] will be set to path[k][j], as it is better to go from i to k, and then k to j. All the vertices will be selected as k. We’ll have 3 nested loops: for k going from 1 to 4, i going from 1 to 4 and j going from 1 to 4. We’re going check:
if distance[i][j] > distance[i][k] + distance[k][j]
distance[i][j] := distance[i][k] + distance[k][j]
path[i][j] := path[k][j]
end ifSo what we’re basically checking is, for every pair of vertices, do we get a shorter distance by going through another vertex? The total number of operations for our graph will be 4 * 4 * 4 = 64. That means we’re going to do this check 64 times. Let’s look at a few of them:
When k = 1, i = 2 and j = 3, distance[i][j] is -2, which is not greater than distance[i][k] + distance[k][j] = -2 + 0 = -2. So it will remain unchanged. Again, when k = 1, i = 4 and j = 2, distance[i][j] = infinity, which is greater than distance[i][k] + distance[k][j] = 1 + 3 = 4. So we put distance[i][j] = 4, and we put path[i][j] = path[k][j] = 1. What this means is, to go from vertex-4 to vertex-2, the path 4->1->2 is shorter than the existing path. This is how we populate both matrices. The calculation for each step is shown here. After making necessary changes, our matrices will look like:
+-----+-----+-----+-----+-----+ +-----+-----+-----+-----+-----+
| | 1 | 2 | 3 | 4 | | | 1 | 2 | 3 | 4 |
+-----+-----+-----+-----+-----+ +-----+-----+-----+-----+-----+
| 1 | 0 | 3 | 1 | 3 | | 1 | N | 1 | 2 | 3 |
+-----+-----+-----+-----+-----+ +-----+-----+-----+-----+-----+
| 2 | 1 | 0 | -2 | 0 | | 2 | 4 | N | 2 | 3 |
+-----+-----+-----+-----+-----+ +-----+-----+-----+-----+-----+
| 3 | 3 | 6 | 0 | 2 | | 3 | 4 | 1 | N | 3 |
+-----+-----+-----+-----+-----+ +-----+-----+-----+-----+-----+
| 4 | 1 | 4 | 2 | 0 | | 4 | 4 | 1 | 2 | N |
+-----+-----+-----+-----+-----+ +-----+-----+-----+-----+-----+
distance pathThis is our shortest distance matrix. For example, the shortest distance from 1 to 4 is 3 and the shortest distance between 4 to 3 is 2. Our pseudo-code will be:
Procedure Floyd-Warshall(Graph):
for k from 1 to V // V denotes the number of vertex
for i from 1 to V
for j from 1 to V
if distance[i][j] > distance[i][k] + distance[k][j]
distance[i][j] := distance[i][k] + distance[k][j]
path[i][j] := path[k][j]
end if
end for
end for
end forPrinting the path:
To print the path, we’ll check the Path matrix. To print the path from u to v, we’ll start from path[u][v]. We’ll set keep changing v = path[u][v] until we find path[u][v] = u and push every values of path[u][v] in a stack. After finding u, we’ll print u and start popping items from the stack and print them. This works because the path matrix stores the value of the vertex which shares the shortest path to v from any other node. The pseudo-code will be:
Procedure PrintPath(source, destination):
s = Stack()
S.push(destination)
while Path[source][destination] is not equal to source
S.push(Path[source][destination])
destination := Path[source][destination]
end while
print -> source
while S is not empty
print -> S.pop
end whileFinding Negative Edge Cycle:
To find out if there is a negative edge cycle, we’ll need to check the main diagonal of distance matrix. If any value on the diagonal is negative, that means there is a negative cycle in the graph.
Complexity:
The complexity of Floyd-Warshall algorithm is O(V³) and the space complexity is: O(V²).