Binary Search Tree - Deletion (C++)

Before starting with deletion I just want to put some lights on what is a Binary search tree(BST), Each node in a BST can have maximum of two nodes(left and right child).The left sub-tree of a node has a key less than or equal to its parent node’s key. The right sub-tree of a node has a key greater than to its parent node’s key.

Deleting a node in a tree while maintaining its Binary search tree property.

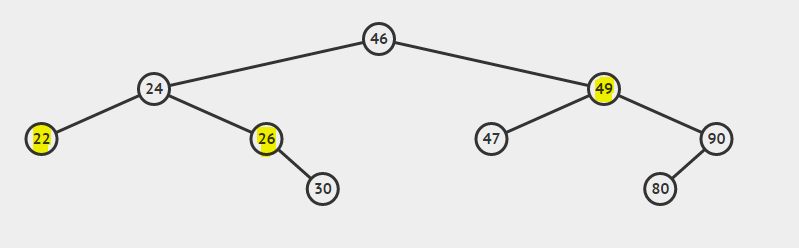
There are three cases to be considered while deleting a node.

• Case 1: Node to be deleted is the leaf node.(Node with value 22).
• Case 2: Node to be deleted has one child.(Node with value 26).
• Case 3: Node to be deleted has both children.(Node with value 49).

Explanation of cases:

1. When the node to be deleted is a leaf node then simply delete the node and pass nullptr to its parent node.
2. When a node to be deleted is having only one child then copy the child value to the node value and delete the child (Converted to case 1)
3. When a node to be delete is having two childs then the minimum from its right sub tree can be copied to the node and then the minimum value can be deleted from the node’s right subtree (Converted to Case 2)

Note: The minimum in the right sub tree can have a maximum of one child and that too right child if it’s having the left child that means it’s not the minimum value or it’s not following BST property.

The structure of a node in a tree and the code for Deletion:

struct node
{
    int data;
    node *left, *right;
};

node* delete_node(node *root, int data)
{
  if(root == nullptr) return root;
  else if(data < root->data) root->left  = delete_node(root->left, data);
  else if(data > root->data) root->right = delete_node(root->right, data);

  else
  {
    if(root->left == nullptr && root->right == nullptr) // Case 1
    {
      free(root);
      root = nullptr;
    }
    else if(root->left == nullptr)       // Case 2
    {
       node* temp = root;
       root= root->right;
       free(temp);
    }
    else if(root->right == nullptr)      // Case 2
    {
       node* temp = root;
       root = root->left;
       free(temp);
    }
    else                                 // Case 3
    {
       node* temp = root->right;

       while(temp->left != nullptr) temp = temp->left;

       root->data = temp->data;
       root->right = delete_node(root->right, temp->data);
    }
  }
  return root;
}

Time complexity of above code is O(h), where h is the height of the tree.