Comparison of the asymptotic notations
suggest changeLet f(n) and g(n) be two functions defined on the set of the positive real numbers, c, c1, c2, n0 are positive real constants.
Notation | f(n) = O(g(n)) | f(n) = Ω(g(n)) | f(n) = Θ(g(n)) | f(n) = o(g(n)) | f(n) = ω(g(n)) |
—— | —— | —— | —— | —— | —— |
Formal definition | ∃ c > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ f(n) ≤ c g(n) | ∃ c > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ c g(n) ≤ f(n) | ∃ c1, c2 > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ c1 g(n) ≤ f(n) ≤ c2 g(n) | ∀ c > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ f(n) < c g(n) | ∀ c > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ c g(n) < f(n) |
Analogy between the asymptotic comparison of f, g and real numbers a, b | a ≤ b | a ≥ b | a = b | a < b | a > b |
Example | 7n + 10 = O(n^2 + n - 9) | n^3 - 34 = Ω(10n^2 - 7n + 1) | 1/2 n^2 - 7n = Θ(n^2) | 5n^2 = o(n^3) | 7n^2 = ω(n) |
Graphic interpretation | | | | | |
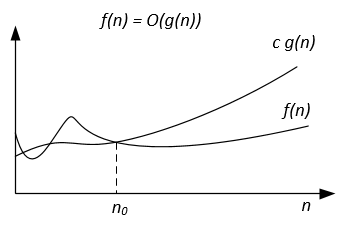
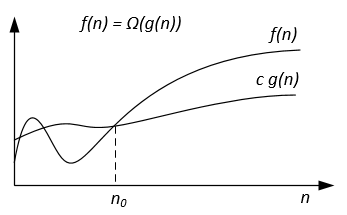
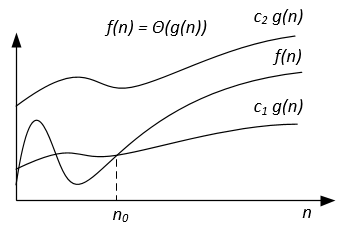
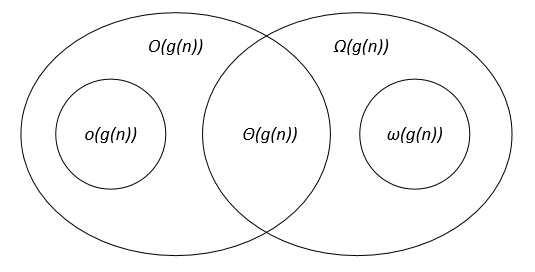
The asymptotic notations can be represented on a Venn diagram as follows:
Links
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein. Introduction to Algorithms.