Let f(n) and g(n) be two functions defined on the set of the positive real numbers, c, c1, c2, n0 are positive real constants.

Notation | f(n) = O(g(n)) | f(n) = Ω(g(n)) | f(n) = Θ(g(n)) | f(n) = o(g(n)) | f(n) = ω(g(n)) | —— | —— | —— | —— | —— | —— | Formal definition | ∃ c > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ f(n) ≤ c g(n) | ∃ c > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ c g(n) ≤ f(n) | ∃ c1, c2 > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ c1 g(n) ≤ f(n) ≤ c2 g(n) | ∀ c > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ f(n) < c g(n) | ∀ c > 0, ∃ n0 > 0 : ∀ n ≥ n0, 0 ≤ c g(n) < f(n) | Analogy between the asymptotic comparison of f, g and real numbers a, b | a ≤ b | a ≥ b | a = b | a < b | a > b | Example | 7n + 10 = O(n^2 + n - 9) | n^3 - 34 = Ω(10n^2 - 7n + 1) | 1/2 n^2 - 7n = Θ(n^2) | 5n^2 = o(n^3) | 7n^2 = ω(n) | Graphic interpretation | | | | | |

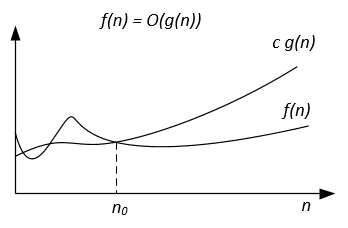
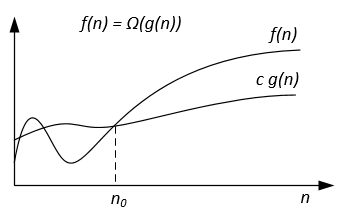
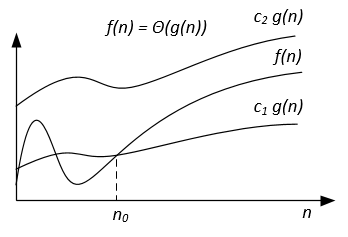
The asymptotic notations can be represented on a Venn diagram as follows:

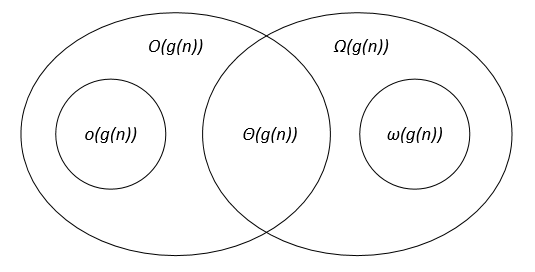
Links

Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, Clifford Stein. Introduction to Algorithms.