Connected Components Of Undirected Graph Using BFS.
suggest changeBFS can be used to find the connected components of an undirected graph. We can also find if the given graph is connected or not. Our subsequent discussion assumes we are dealing with undirected graphs.The definition of a connected graph is:
A graph is connected if there is a path between every pair of vertices.
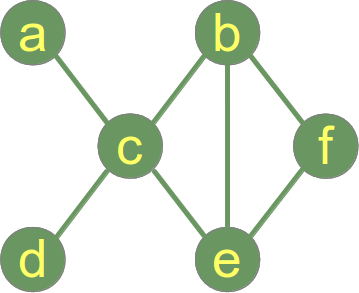
Following is a connected graph.
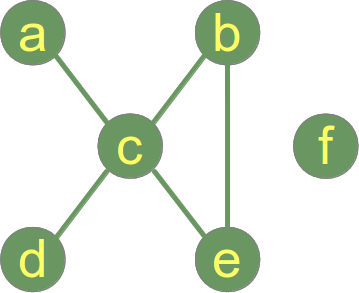
Following graph is not connected and has 2 connected components:
- Connected Component 1: {a,b,c,d,e}
- Connected Component 2: {f}
BFS is a graph traversal algorithm. So starting from a random source node, if on termination of algorithm, all nodes are visited, then the graph is connected,otherwise it is not connected.
PseudoCode for the algorithm.
boolean isConnected(Graph g)
{
BFS(v)//v is a random source node.
if(allVisited(g))
{
return true;
}
else return false;
}C implementation for finding the whether an undirected graph is connected or not:
#include<stdio.h>
#include<stdlib.h>
#define MAXVERTICES 100
void enqueue(int);
int deque();
int isConnected(char **graph,int noOfVertices);
void BFS(char **graph,int vertex,int noOfVertices);
int count = 0;
//Queue node depicts a single Queue element
//It is NOT a graph node.
struct node
{
int v;
struct node *next;
};
typedef struct node Node;
typedef struct node *Nodeptr;
Nodeptr Qfront = NULL;
Nodeptr Qrear = NULL;
char *visited;//array that keeps track of visited vertices.
int main()
{
int n,e;//n is number of vertices, e is number of edges.
int i,j;
char **graph;//adjacency matrix
printf("Enter number of vertices:");
scanf("%d",&n);
if(n < 0 || n > MAXVERTICES)
{
fprintf(stderr, "Please enter a valid positive integer from 1 to %d",MAXVERTICES);
return -1;
}
graph = malloc(n * sizeof(char *));
visited = malloc(n*sizeof(char));
for(i = 0;i < n;++i)
{
graph[i] = malloc(n*sizeof(int));
visited[i] = 'N';//initially all vertices are not visited.
for(j = 0;j < n;++j)
graph[i][j] = 0;
}
printf("enter number of edges and then enter them in pairs:");
scanf("%d",&e);
for(i = 0;i < e;++i)
{
int u,v;
scanf("%d%d",&u,&v);
graph[u-1][v-1] = 1;
graph[v-1][u-1] = 1;
}
if(isConnected(graph,n))
printf("The graph is connected");
else printf("The graph is NOT connected\n");
}
void enqueue(int vertex)
{
if(Qfront == NULL)
{
Qfront = malloc(sizeof(Node));
Qfront->v = vertex;
Qfront->next = NULL;
Qrear = Qfront;
}
else
{
Nodeptr newNode = malloc(sizeof(Node));
newNode->v = vertex;
newNode->next = NULL;
Qrear->next = newNode;
Qrear = newNode;
}
}
int deque()
{
if(Qfront == NULL)
{
printf("Q is empty , returning -1\n");
return -1;
}
else
{
int v = Qfront->v;
Nodeptr temp= Qfront;
if(Qfront == Qrear)
{
Qfront = Qfront->next;
Qrear = NULL;
}
else
Qfront = Qfront->next;
free(temp);
return v;
}
}
int isConnected(char **graph,int noOfVertices)
{
int i;
//let random source vertex be vertex 0;
BFS(graph,0,noOfVertices);
for(i = 0;i < noOfVertices;++i)
if(visited[i] == 'N')
return 0;//0 implies false;
return 1;//1 implies true;
}
void BFS(char **graph,int v,int noOfVertices)
{
int i,vertex;
visited[v] = 'Y';
enqueue(v);
while((vertex = deque()) != -1)
{
for(i = 0;i < noOfVertices;++i)
if(graph[vertex][i] == 1 && visited[i] == 'N')
{
enqueue(i);
visited[i] = 'Y';
}
}
}For Finding all the Connected components of an undirected graph, we only need to add 2 lines of code to the BFS function. The idea is to call BFS function until all vertices are visited.
The lines to be added are:
printf("\nConnected component %d\n",++count);
//count is a global variable initialized to 0
//add this as first line to BFS functionAND
printf("%d ",vertex+1);
add this as first line of while loop in BFSand we define the following function:
void listConnectedComponents(char **graph,int noOfVertices)
{
int i;
for(i = 0;i < noOfVertices;++i)
{
if(visited[i] == 'N')
BFS(graph,i,noOfVertices);
}
}