Detecting Negative Cycle in a Graph

To understand this example, it is recommended to have a brief idea about Bellman-Ford algorithm which can be found here

Using Bellman-Ford algorithm, we can detect if there is a negative cycle in our graph. We know that, to find out the shortest path, we need to relax all the edges of the graph (V-1) times, where V is the number of vertices in a graph. We have already seen that in this example, after (V-1) iterations, we can’t update d[], no matter how many iterations we do. Or can we?

If there is a negative cycle in a graph, even after (V-1) iterations, we can update d[]. This happens because for every iteration, traversing through the negative cycle always decreases the cost of the shortest path. This is why Bellman-Ford algorithm limits the number of iterations to (V-1). If we used Dijkstra’s Algorithm here, we’d be stuck in an endless loop. However, let’s concentrate on finding negative cycle.

Let’s assume, we have a graph:

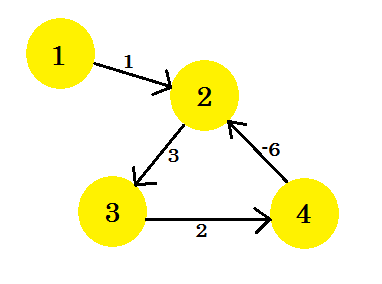
Let’s pick vertex 1 as the source. After applying Bellman-Ford’s single source shortest path algorithm to the graph, we’ll find out the distances from the source to all the other vertices.

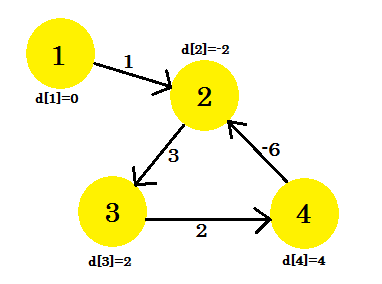
This is how the graph looks like after (V-1) = 3 iterations. It should be the result since there are 4 edges, we need at most 3 iterations to find out the shortest path. So either this is the answer, or there is a negative weight cycle in the graph. To find that, after (V-1) iterations, we do one more final iteration and if the distance continues to decrease, it means that there is definitely a negative weight cycle in the graph.

For this example: if we check 2-3, d[2] + cost[2][3] will give us 1 which is less than d[3]. So we can conclude that there is a negative cycle in our graph.

So how do we find out the negative cycle? We do a bit modification to Bellman-Ford procedure:

Procedure NegativeCycleDetector(Graph, source):
n := number of vertices in Graph
for i from 1 to n
    d[i] := infinity
end for
d[source] := 0
for i from 1 to n-1
    flag := false
    for all edges from (u,v) in Graph
        if d[u] + cost[u][v] < d[v]
            d[v] := d[u] + cost[u][v]
            flag := true
        end if
    end for
    if flag == false
        break
end for
for all edges from (u,v) in Graph
    if d[u] + cost[u][v] < d[v]
        Return "Negative Cycle Detected"
    end if
end for
Return "No Negative Cycle"

This is how we find out if there is a negative cycle in a graph. We can also modify Bellman-Ford Algorithm to keep track of negative cycles.