Introduction To Graph Theory
suggest changeGraph Theory is the study of graphs, which are mathematical structures used to model pairwise relations between objects.
Did you know, almost all the problems of planet Earth can be converted into problems of Roads and Cities, and solved? Graph Theory was invented many years ago, even before the invention of computer. Leonhard Euler wrote a paper on the Seven Bridges of Königsberg which is regarded as the first paper of Graph Theory. Since then, people have come to realize that if we can convert any problem to this City-Road problem, we can solve it easily by Graph Theory.
Graph Theory has many applications.One of the most common application is to find the shortest distance between one city to another. We all know that to reach your PC, this web-page had to travel many routers from the server. Graph Theory helps it to find out the routers that needed to be crossed. During war, which street needs to be bombarded to disconnect the capital city from others, that too can be found out using Graph Theory.
Let us first learn some basic definitions on Graph Theory.
Graph:
Let’s say, we have 6 cities. We mark them as 1, 2, 3, 4, 5, 6. Now we connect the cities that have roads between each other.
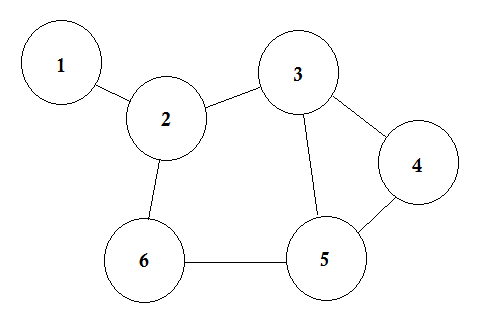
This is a simple graph where some cities are shown with the roads that are connecting them. In Graph Theory, we call each of these cities Node or Vertex and the roads are called Edge. Graph is simply a connection of these nodes and edges.
A node can represent a lot of things. In some graphs, nodes represent cities, some represent airports, some represent a square in a chessboard. Edge represents the relation between each nodes. That relation can be the time to go from one airport to another, the moves of a knight from one square to all the other squares etc.
Path of Knight in a Chessboard
In simple words, a Node represents any object and Edge represents the relation between two objects.
Adjacent Node:
If a node A shares an edge with node B, then B is considered to be adjacent to A. In other words, if two nodes are directly connected, they are called adjacent nodes. One node can have multiple adjacent nodes.
Directed and Undirected Graph:
In directed graphs, the edges have direction signs on one side, that means the edges are Unidirectional. On the other hand, the edges of undirected graphs have direction signs on both sides, that means they are Bidirectional. Usually undirected graphs are represented with no signs on the either sides of the edges.
Let’s assume there is a party going on. The people in the party are represented by nodes and there is an edge between two people if they shake hands. Then this graph is undirected because any person A shake hands with person B if and only if B also shakes hands with A. In contrast, if the edges from a person A to another person B corresponds to A’s admiring B, then this graph is directed, because admiration is not necessarily reciprocated. The former type of graph is called an undirected graph and the edges are called undirected edges while the latter type of graph is called a directed graph and the edges are called directed edges.
Weighted and Unweighted Graph:
A weighted graph is a graph in which a number (the weight) is assigned to each edge. Such weights might represent for example costs, lengths or capacities, depending on the problem at hand.
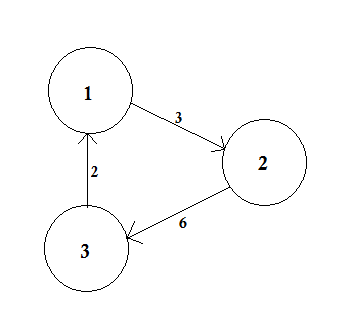
An unweighted graph is simply the opposite. We assume that, the weight of all the edges are same (presumably 1).
Path:
A path represents a way of going from one node to another. It consists of sequence of edges. There can be multiple paths between two nodes.
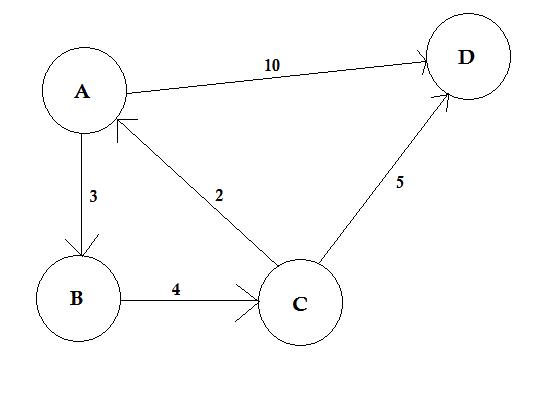
In the example above, there are two paths from A to D. A->B, B->C, C->D is one path. The cost of this path is 3 + 4 + 2 = 9. Again, there’s another path A->D. The cost of this path is 10. The path that costs the lowest is called shortest path.
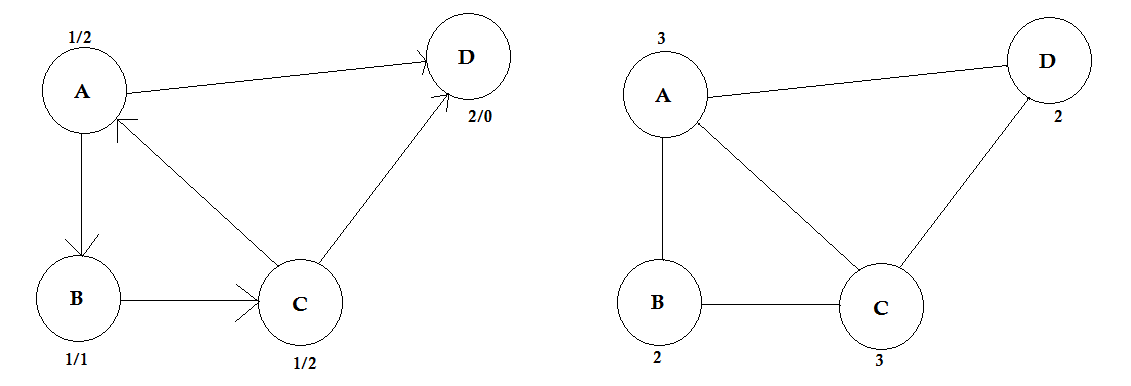
Degree:
The degree of a vertex is the number of edges that are connected to it. If there’s any edge that connects to the vertex at both ends (a loop) is counted twice.
In directed graphs, the nodes have two types of degrees:
- In-degree: The number of edges that point to the node.
- Out-degree: The number of edges that point from the node to other nodes.
For undirected graphs, they are simply called degree.
Some Algorithms Related to Graph Theory
- Bellman–Ford algorithm
- Dijkstra’s algorithm
- Ford–Fulkerson algorithm
- Kruskal’s algorithm
- Nearest neighbour algorithm
- Prim’s algorithm
- Depth-first search
- Breadth-first search