Quicksort Basics

Quicksort is a sorting algorithm that picks an element (“the pivot”) and reorders the array forming two partitions such that all elements less than the pivot come before it and all elements greater come after. The algorithm is then applied recursively to the partitions until the list is sorted.

1. Lomuto partition scheme mechanism :

This scheme chooses a pivot which is typically the last element in the array. The algorithm maintains the index to put the pivot in variable i and each time it finds an element less than or equal to pivot, this index is incremented and that element would be placed before the pivot.

partition(A, low, high) is
pivot := A[high]
i := low
for j := low to high – 1 do
    if A[j] ≤ pivot then
        swap A[i] with A[j]
        i := i + 1
swap A[i] with A[high]
return i

Quick Sort mechanism :

quicksort(A, low, high) is
if low < high then
    p := partition(A, low, high)
    quicksort(A, low, p – 1)
    quicksort(A, p + 1, high)

Example of quick sort:

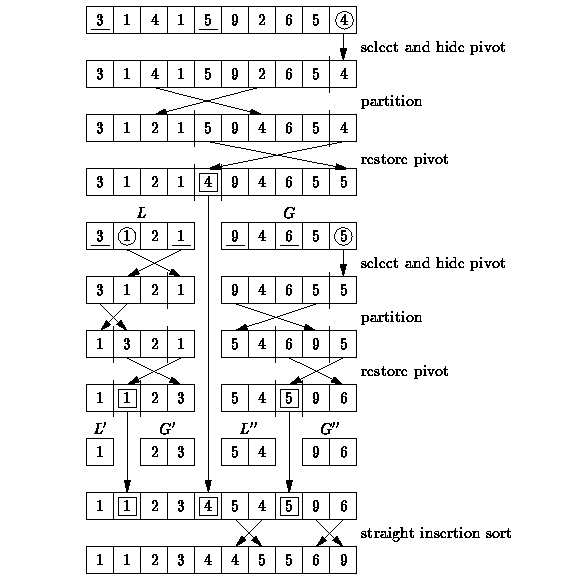
2. Hoare partition scheme:

It uses two indices that start at the ends of the array being partitioned, then move toward each other, until they detect an inversion: a pair of elements, one greater or equal than the pivot, one lesser or equal, that are in the wrong order relative to each other. The inverted elements are then swapped. When the indices meet, the algorithm stops and returns the final index. Hoare’s scheme is more efficient than Lomuto’s partition scheme because it does three times fewer swaps on average, and it creates efficient partitions even when all values are equal.

quicksort(A, lo, hi) is
if lo < hi then
    p := partition(A, lo, hi)
    quicksort(A, lo, p)
    quicksort(A, p + 1, hi)

Partition :

partition(A, lo, hi) is
pivot := A[lo]
i := lo - 1
j := hi + 1
loop forever
    do:
        i := i + 1
    while A[i] < pivot do
    
    do:
        j := j - 1
    while A[j] > pivot do
    
    if i >= j then
        return j
    
    swap A[i] with A[j]