Radix 2 FFT
suggest changeThe simplest and perhaps best-known method for computing the FFT is the Radix-2 Decimation in Time algorithm. The Radix-2 FFT works by decomposing an N point time domain signal into N time domain signals each composed of a single point.
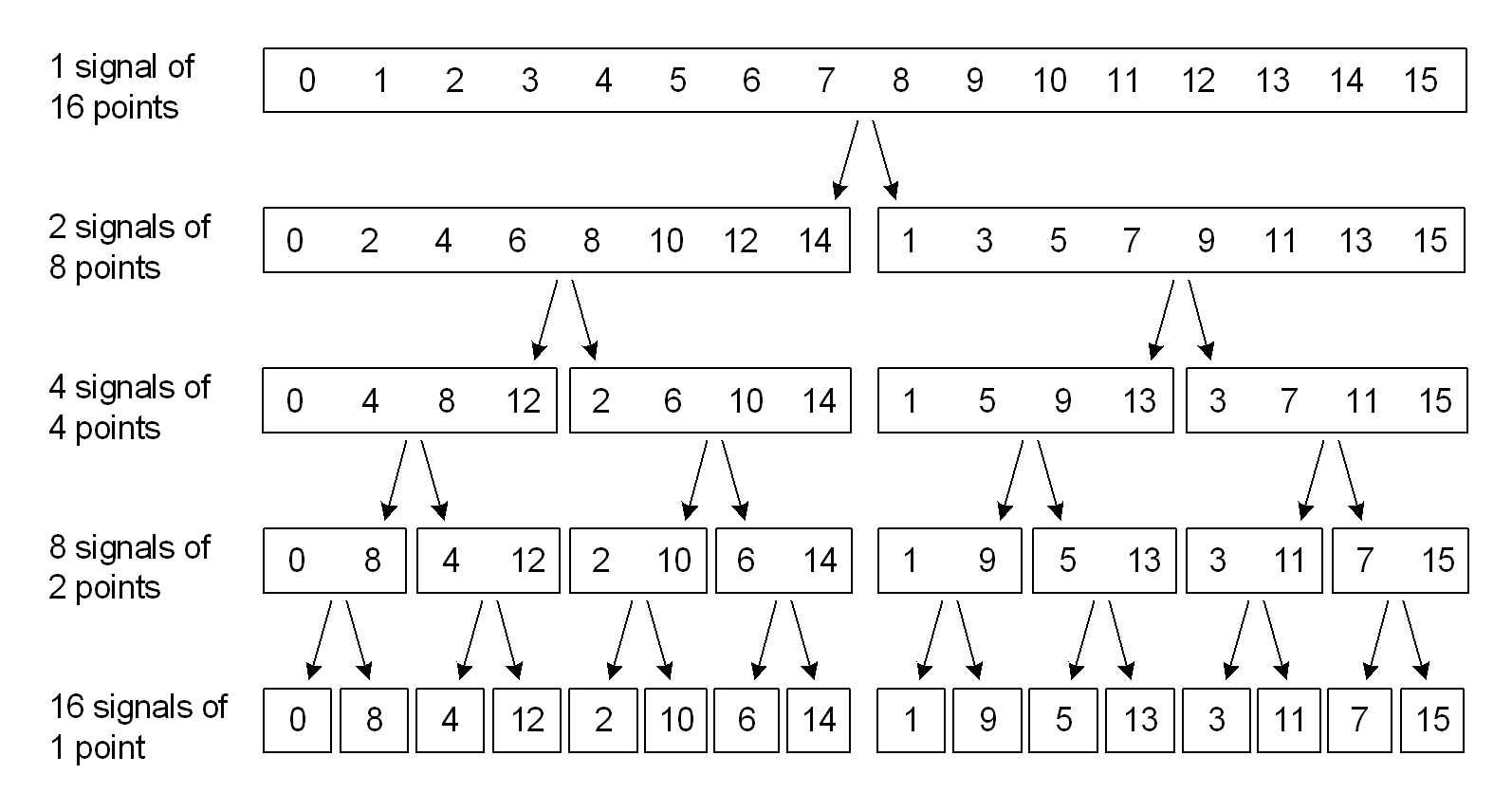
Signal decomposition, or ‘decimation in time’ is achieved by bit reversing the indices for the array of time domain data. Thus, for a sixteen-point signal, sample 1 (Binary 0001) is swapped with sample 8 (1000), sample 2 (0010) is swapped with 4 (0100) and so on. Sample swapping using the bit reverse technique can be achieved simply in software, but limits the use of the Radix 2 FFT to signals of length N = 2^M.
The value of a 1-point signal in the time domain is equal to its value in the frequency domain, thus this array of decomposed single time-domain points requires no transformation to become an array of frequency domain points. The N single points; however, need to be reconstructed into one N-point frequency spectra. Optimal reconstruction of the complete frequency spectrum is performed using butterfly calculations. Each reconstruction stage in the Radix-2 FFT performs a number of two point butterflies, using a similar set of exponential weighting functions, Wn^R.
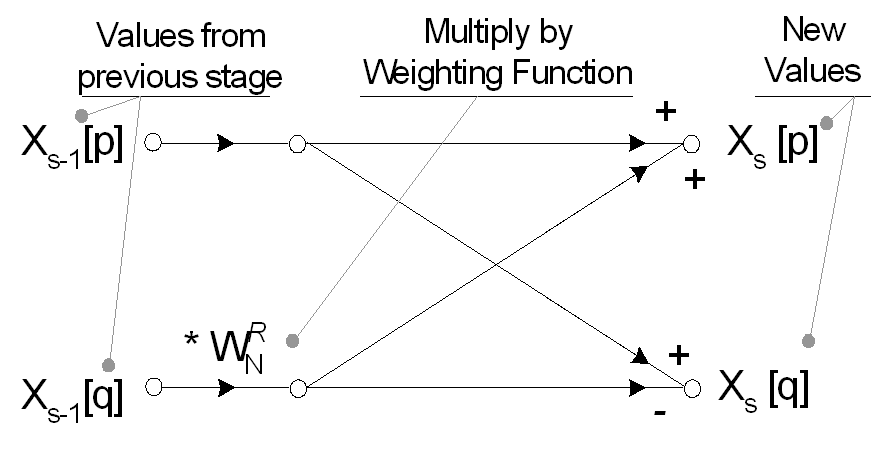
The FFT removes redundant calculations in the Discrete Fourier Transform by exploiting the periodicity of Wn^R. Spectral reconstruction is completed in log2(N) stages of butterfly calculations giving X[K]; the real and imaginary frequency domain data in rectangular form. To convert to magnitude and phase (polar coordinates) requires finding the absolute value, √(Re2 + Im2), and argument, tan-1(Im/Re).

The complete butterfly flow diagram for an eight point Radix 2 FFT is shown below. Note the input signals have previously been reordered according to the decimation in time procedure outlined previously.
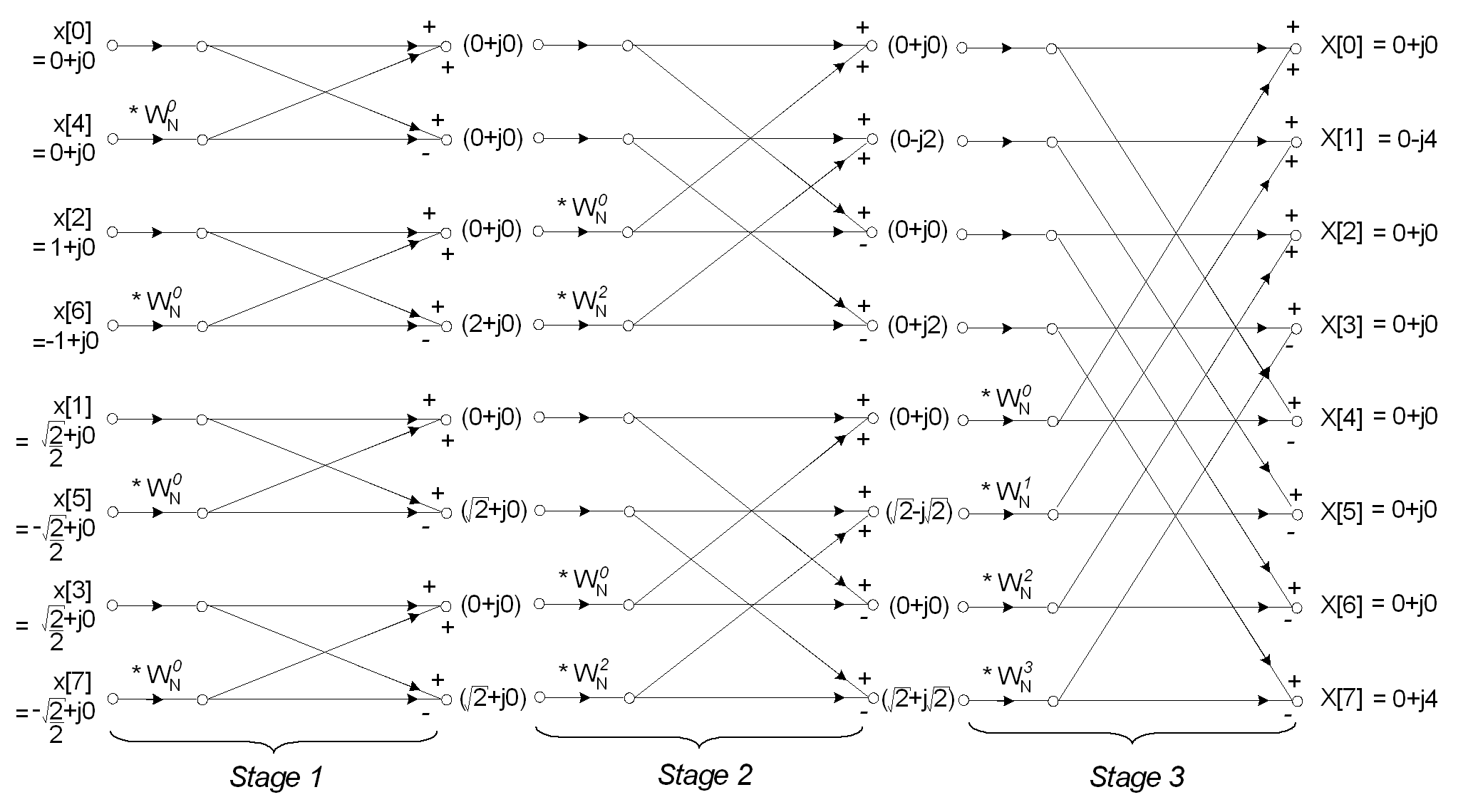
The FFT typically operates on complex inputs and produces a complex output. For real signals, the imaginary part may be set to zero and real part set to the input signal, x[n], however many optimisations are possible involving the transformation of real-only data. Values of Wn^R used throughout the reconstruction can be determined using the exponential weighting equation.
The value of R (the exponential weighting power) is determined the current stage in the spectral reconstruction and the current calculation within a particular butterfly.
Code Example (C/C++)
A C/C++ code sample for computing the Radix 2 FFT can be found below. This is a simple implementation which works for any size N where N is a power of 2. It is approx 3x slower than the fastest FFTw implementation, but still a very good basis for future optimisation or for learning about how this algorithm works.
#include <math.h>
#define PI 3.1415926535897932384626433832795 // PI for sine/cos calculations
#define TWOPI 6.283185307179586476925286766559 // 2*PI for sine/cos calculations
#define Deg2Rad 0.017453292519943295769236907684886 // Degrees to Radians factor
#define Rad2Deg 57.295779513082320876798154814105 // Radians to Degrees factor
#define log10_2 0.30102999566398119521373889472449 // Log10 of 2
#define log10_2_INV 3.3219280948873623478703194294948 // 1/Log10(2)
// complex variable structure (double precision)
struct complex
{
public:
double Re, Im; // Not so complicated after all
};
// Returns true if N is a power of 2
bool isPwrTwo(int N, int *M)
{
*M = (int)ceil(log10((double)N) * log10_2_INV);// M is number of stages to perform. 2^M = N
int NN = (int)pow(2.0, *M);
if ((NN != N) || (NN == 0)) // Check N is a power of 2.
return false;
return true;
}
void rad2FFT(int N, complex *x, complex *DFT)
{
int M = 0;
// Check if power of two. If not, exit
if (!isPwrTwo(N, &M))
throw "Rad2FFT(): N must be a power of 2 for Radix FFT";
// Integer Variables
int BSep; // BSep is memory spacing between butterflies
int BWidth; // BWidth is memory spacing of opposite ends of the butterfly
int P; // P is number of similar Wn's to be used in that stage
int j; // j is used in a loop to perform all calculations in each stage
int stage = 1; // stage is the stage number of the FFT. There are M stages in total (1 to M).
int HiIndex; // HiIndex is the index of the DFT array for the top value of each butterfly calc
unsigned int iaddr; // bitmask for bit reversal
int ii; // Integer bitfield for bit reversal (Decimation in Time)
int MM1 = M - 1;
unsigned int i;
int l;
unsigned int nMax = (unsigned int)N;
// Double Precision Variables
double TwoPi_N = TWOPI / (double)N; // constant to save computational time. = 2*PI / N
double TwoPi_NP;
// complex Variables (See 'struct complex')
complex WN; // Wn is the exponential weighting function in the form a + jb
complex TEMP; // TEMP is used to save computation in the butterfly calc
complex *pDFT = DFT; // Pointer to first elements in DFT array
complex *pLo; // Pointer for lo / hi value of butterfly calcs
complex *pHi;
complex *pX; // Pointer to x[n]// Decimation In Time - x[n] sample sorting
for (i = 0; i < nMax; i++, DFT++)
{
pX = x + i; // Calculate current x[n] from base address *x and index i.
ii = 0; // Reset new address for DFT[n]
iaddr = i; // Copy i for manipulations
for (l = 0; l < M; l++) // Bit reverse i and store in ii...
{
if (iaddr & 0x01) // Detemine least significant bit
ii += (1 << (MM1 - l)); // Increment ii by 2^(M-1-l) if lsb was 1
iaddr >>= 1; // right shift iaddr to test next bit. Use logical operations for speed increase
if (!iaddr)
break;
}
DFT = pDFT + ii; // Calculate current DFT[n] from base address *pDFT and bit reversed index ii
DFT->Re = pX->Re; // Update the complex array with address sorted time domain signal x[n]
DFT->Im = pX->Im; // NB: Imaginary is always zero
}
// FFT Computation by butterfly calculation
for (stage = 1; stage <= M; stage++) // Loop for M stages, where 2^M = N
{
BSep = (int)(pow(2, stage)); // Separation between butterflies = 2^stage
P = N / BSep; // Similar Wn's in this stage = N/Bsep
BWidth = BSep / 2; // Butterfly width (spacing between opposite points) = Separation / 2.
TwoPi_NP = TwoPi_N*P;
for (j = 0; j < BWidth; j++) // Loop for j calculations per butterfly
{
if (j != 0) // Save on calculation if R = 0, as WN^0 = (1 + j0)
{
//WN.Re = cos(TwoPi_NP*j)
WN.Re = cos(TwoPi_N*P*j); // Calculate Wn (Real and Imaginary)
WN.Im = -sin(TwoPi_N*P*j);
}
for (HiIndex = j; HiIndex < N; HiIndex += BSep) // Loop for HiIndex Step BSep butterflies per stage
{
pHi = pDFT + HiIndex; // Point to higher value
pLo = pHi + BWidth; // Point to lower value (Note VC++ adjusts for spacing between elements)
if (j != 0) // If exponential power is not zero...
{
//CMult(pLo, &WN, &TEMP); // Perform complex multiplication of Lovalue with Wn
TEMP.Re = (pLo->Re * WN.Re) - (pLo->Im * WN.Im);
TEMP.Im = (pLo->Re * WN.Im) + (pLo->Im * WN.Re);
//CSub (pHi, &TEMP, pLo);
pLo->Re = pHi->Re - TEMP.Re; // Find new Lovalue (complex subtraction)
pLo->Im = pHi->Im - TEMP.Im;
//CAdd (pHi, &TEMP, pHi); // Find new Hivalue (complex addition)
pHi->Re = (pHi->Re + TEMP.Re);
pHi->Im = (pHi->Im + TEMP.Im);
}
else
{
TEMP.Re = pLo->Re;
TEMP.Im = pLo->Im;
//CSub (pHi, &TEMP, pLo);
pLo->Re = pHi->Re - TEMP.Re; // Find new Lovalue (complex subtraction)
pLo->Im = pHi->Im - TEMP.Im;
//CAdd (pHi, &TEMP, pHi); // Find new Hivalue (complex addition)
pHi->Re = (pHi->Re + TEMP.Re);
pHi->Im = (pHi->Im + TEMP.Im);
}
}
}
}pLo = 0; // Null all pointers
pHi = 0;
pDFT = 0;
DFT = 0;
pX = 0;
}