Storing Graphs (Adjacency Matrix)

To store a graph, two methods are common:

Adjacency Matrix
Adjacency List

An adjacency matrix is a square matrix used to represent a finite graph. The elements of the matrix indicate whether pairs of vertices are adjacent or not in the graph.

Adjacent means ‘next to or adjoining something else’ or to be beside something. For example, your neighbors are adjacent to you. In graph theory, if we can go to node B from node A, we can say that node B is adjacent to node A. Now we will learn about how to store which nodes are adjacent to which one via Adjacency Matrix. This means, we will represent which nodes share edge between them. Here matrix means 2D array.

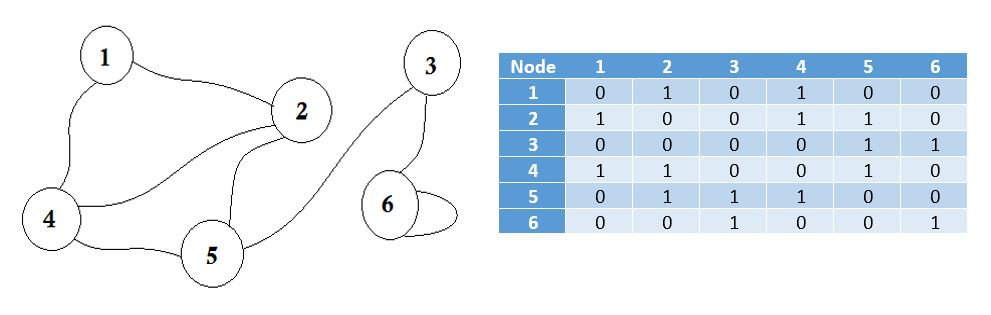
Here you can see a table beside the graph, this is our adjacency matrix. Here Matrix[i][j] = 1 represents there is an edge between i and j. If there’s no edge, we simply put Matrix[i][j] = 0.

These edges can be weighted, like it can represent the distance between two cities. Then we’ll put the value in Matrix[i][j] instead of putting 1.

The graph described above is Bidirectional or Undirected, that means, if we can go to node 1 from node 2, we can also go to node 2 from node 1. If the graph was Directed, then there would’ve been arrow sign on one side of the graph. Even then, we could represent it using adjacency matrix.

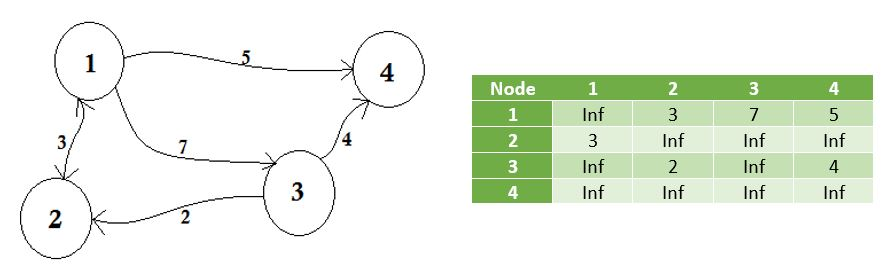
We represent the nodes that don’t share edge by infinity. One thing to be noticed is that, if the graph is undirected, the matrix becomes symmetric.

The pseudo-code to create the matrix:

Procedure AdjacencyMatrix(N):    //N represents the number of nodes
Matrix[N][N]
for i from 1 to N
    for j from 1 to N
        Take input -> Matrix[i][j]
    endfor
endfor

We can also populate the Matrix using this common way:

Procedure AdjacencyMatrix(N, E):    // N -> number of nodes
Matrix[N][E]                        // E -> number of edges
for i from 1 to E
    input -> n1, n2, cost
    Matrix[n1][n2] = cost
    Matrix[n2][n1] = cost
endfor

For directed graphs, we can remove Matrix[n2][n1] = cost line.

The drawbacks of using Adjacency Matrix:

Memory is a huge problem. No matter how many edges are there, we will always need N * N sized matrix where N is the number of nodes. If there are 10000 nodes, the matrix size will be 4 * 10000 * 10000 around 381 megabytes. This is a huge waste of memory if we consider graphs that have a few edges.

Suppose we want to find out to which node we can go from a node u. We’ll need to check the whole row of u, which costs a lot of time.

The only benefit is that, we can easily find the connection between u-v nodes, and their cost using Adjacency Matrix.

Java code implemented using above pseudo-code:

import java.util.Scanner;
 
public class Represent_Graph_Adjacency_Matrix 
{
    private final int vertices;
    private int[][] adjacency_matrix;
 
    public Represent_Graph_Adjacency_Matrix(int v) 
    {
        vertices = v;
        adjacency_matrix = new int[vertices + 1][vertices + 1];
    }
 
    public void makeEdge(int to, int from, int edge) 
    {
        try 
        {
            adjacency_matrix[to][from] = edge;
        }
        catch (ArrayIndexOutOfBoundsException index) 
        {
            System.out.println("The vertices does not exists");
        }
    }
 
    public int getEdge(int to, int from) 
    {
        try 
        {
            return adjacency_matrix[to][from];
        }
        catch (ArrayIndexOutOfBoundsException index) 
        {
            System.out.println("The vertices does not exists");
        }
        return -1;
    }
 
    public static void main(String args[]) 
    {
        int v, e, count = 1, to = 0, from = 0;
        Scanner sc = new Scanner(System.in);
        Represent_Graph_Adjacency_Matrix graph;
        try 
        {
            System.out.println("Enter the number of vertices: ");
            v = sc.nextInt();
            System.out.println("Enter the number of edges: ");
            e = sc.nextInt();
 
            graph = new Represent_Graph_Adjacency_Matrix(v);
 
            System.out.println("Enter the edges: <to> <from>");
            while (count <= e) 
            {
                to = sc.nextInt();
                from = sc.nextInt();
 
                graph.makeEdge(to, from, 1);
                count++;
            }
 
            System.out.println("The adjacency matrix for the given graph is: ");
            System.out.print("  ");
            for (int i = 1; i <= v; i++)
                System.out.print(i + " ");
            System.out.println();
 
            for (int i = 1; i <= v; i++) 
            {
                System.out.print(i + " ");
                for (int j = 1; j <= v; j++) 
                    System.out.print(graph.getEdge(i, j) + " ");
                System.out.println();
            }
 
        }
        catch (Exception E) 
        {
            System.out.println("Somthing went wrong");
        }
 
        sc.close();
    }
}

Running the code: Save the file and compile using javac Represent_Graph_Adjacency_Matrix.java

Example:

$ java Represent_Graph_Adjacency_Matrix
Enter the number of vertices:
4
Enter the number of edges:
6
Enter the edges: <to> <from>
1 1
3 4
2 3
1 4
2 4
1 2
The adjacency matrix for the given graph is:
  1 2 3 4
1 1 1 0 1
2 0 0 1 1
3 0 0 0 1
4 0 0 0 0

Found a mistake? Have a question or improvement idea? Let me know.

Table Of Contents