Why do we need to relax all the edges at most V-1 times

To understand this example, it is recommended to have a brief idea on Bellman-Ford single source shortest path algorithm which can be found here

In Bellman-Ford algorithm, to find out the shortest path, we need to relax all the edges of the graph. This process is repeated at most (V-1) times, where V is the number of vertices in the graph.

The number of iterations needed to find out the shortest path from source to all other vertices depends on the order that we select to relax the edges.

Let’s take a look at an example:

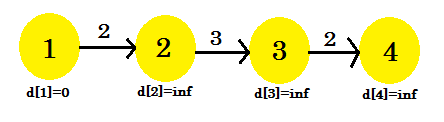
Here, the source vertex is 1. We will find out the shortest distance between the source and all the other vertices. We can clearly see that, to reach vertex 4, in the worst case, it’ll take (V-1) edges. Now depending on the order in which the edges are discovered, it might take (V-1) times to discover vertex 4. Didn’t get it? Let’s use Bellman-Ford algorithm to find out the shortest path here:

We’re going to use this sequence:

+--------+--------+--------+--------+
| Serial |    1   |    2   |    3   |
+--------+--------+--------+--------+
|  Edge  |  3->4  |  2->3  |  1->2  |
+--------+--------+--------+--------+

For our first iteration:

1. d[3] + cost[3][4] = infinity. It won’t change anything.
2. d[2] + cost[2][3] = infinity. It won’t change anything.
3. d[1] + cost[1][2] = 2 < d[2]. d[2] = 2. parent[2] = 1.

We can see that our relaxation process only changed d[2]. Our graph will look like:

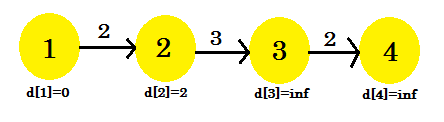
Second iteration:

1. d[3] + cost[3][4] = infinity. It won’t change anything.
2. d[2] + cost[2][3] = 5 < d[3]. d[3] = 5. parent[3] = 2.
3. It won’t be changed.

This time the relaxation process changed d[3]. Our graph will look like:

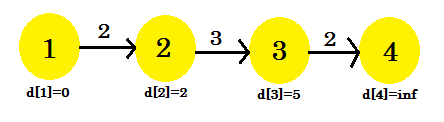
Third iteration:

1. d[3] + cost[3][4] = 7 < d[4]. d[4] = 7. parent[4] = 3.
2. It won’t be changed.
3. It won’t be changed.

Our third iteration finally found out the shortest path to 4 from 1. Our graph will look like:

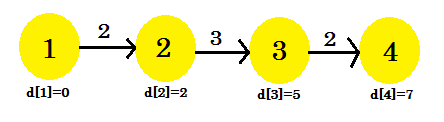
So, it took 3 iterations to find out the shortest path. After this one, no matter how many times we relax the edges, the values in d[] will remain the same. Now, if we considered another sequence:

+--------+--------+--------+--------+
| Serial |    1   |    2   |    3   |
+--------+--------+--------+--------+
|  Edge  |  1->2  |  2->3  |  3->4  |
+--------+--------+--------+--------+

We’d get:

1. d[1] + cost[1][2] = 2 < d[2]. d[2] = 2.
2. d[2] + cost[2][3] = 5 < d[3]. d[3] = 5.
3. d[3] + cost[3][4] = 7 < d[4]. d[4] = 5.

Our very first iteration has found the shortest path from source to all the other nodes. Another sequence 1->2, 3->4, 2->3 is possible, which will give us shortest path after 2 iterations. We can come to the decision that, no matter how we arrange the sequence, it won’t take more than 3 iterations to find out shortest path from the source in this example.

We can conclude that, for the best case, it’ll take 1 iteration to find out the shortest path from source. For the worst case, it’ll take (V-1) iterations, which is why we repeat the process of relaxation (V-1) times.