Iterating through an array efficiently and row-major order
suggest changeArrays in C can be seen as a contiguous chunk of memory. More precisely, the last dimension of the array is the contiguous part. We call this the row-major order. Understanding this and the fact that a cache fault loads a complete cache line into the cache when accessing uncached data to prevent subsequent cache faults, we can see why accessing an array of dimension 10000x10000 with array[0][0] would potentially load array[0][1] in cache, but accessing array[1][0] right after would generate a second cache fault, since it is sizeof(type)*10000 bytes away from array[0][0], and therefore certainly not on the same cache line. Which is why iterating like this is inefficient:
#define ARRLEN 10000
int array[ARRLEN][ARRLEN];
size_t i, j;
for (i = 0; i < ARRLEN; ++i)
{
for(j = 0; j < ARRLEN; ++j)
{
array[j][i] = 0;
}
}And iterating like this is more efficient:
#define ARRLEN 10000
int array[ARRLEN][ARRLEN];
size_t i, j;
for (i = 0; i < ARRLEN; ++i)
{
for(j = 0; j < ARRLEN; ++j)
{
array[i][j] = 0;
}
}In the same vein, this is why when dealing with an array with one dimension and multiple indexes (let’s say 2 dimensions here for simplicity with indexes i and j) it is important to iterate through the array like this:
#define DIM_X 10
#define DIM_Y 20
int array[DIM_X*DIM_Y];
size_t i, j;
for (i = 0; i < DIM_X; ++i)
{
for(j = 0; j < DIM_Y; ++j)
{
array[i*DIM_Y+j] = 0;
}
}Or with 3 dimensions and indexes i,j and k:
#define DIM_X 10
#define DIM_Y 20
#define DIM_Z 30
int array[DIM_X*DIM_Y*DIM_Z];
size_t i, j, k;
for (i = 0; i < DIM_X; ++i)
{
for(j = 0; j < DIM_Y; ++j)
{
for (k = 0; k < DIM_Z; ++k)
{
array[i*DIM_Y*DIM_Z+j*DIM_Z+k] = 0;
}
}
}Or in a more generic way, when we have an array with N1 x N2 x … x Nd elements, d dimensions and indices noted as n1,n2,…,nd the offset is calculated like this
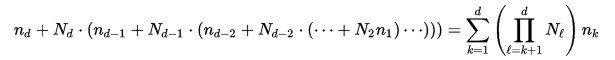
Picture/formula taken from: https://en.wikipedia.org/wiki/Row-major_order